Komposisi Fungsi
dikenal juga dengan penggandaan atau perkalian fungsi. Jika dua fungsi
digandakan yaitu fungsi f dan fungsi g, ditulis g o f jika dan hanya
jika kodomain f subset dari domain g. Secara matematis dapat ditulis
sebagai berikut.
Definisi :
Misalkan f : A 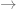 B dan g : C
B dan g : C 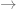 D adalah suatu fungsi sehingga Rf
D adalah suatu fungsi sehingga Rf  Df. Komposisi Fungsi f dan g, dengan notasi g o f, didefinisikan dengan (g o f)(x) = g(f(x)),
Df. Komposisi Fungsi f dan g, dengan notasi g o f, didefinisikan dengan (g o f)(x) = g(f(x)), 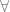 x
x  Df.
Df.
Apabila ditulis dalam bentuk diagram maka akan menjadi seperti digambar dibawah ini.
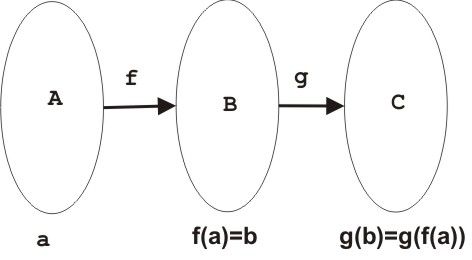
Secara sederhana bahwa (f o g)(x) ada jika range g (Rg) berada pada domain f (Df) dan (g o f)(x) ada jika range f (Rf) berada pada domain g (Dg).
Contoh 1 :
Misalkan f : 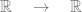 dengan f(x) = 2x dan g :
dengan f(x) = 2x dan g : 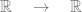 dengan g(x) = x3. Apakah fungsi g o f dan dapat didefinisikan? Jika iya, tentukan formula g o f dan f o g.
dengan g(x) = x3. Apakah fungsi g o f dan dapat didefinisikan? Jika iya, tentukan formula g o f dan f o g.
Penyelesaian :
Kasus g o f
Karena Rf 
 = Dg maka komposisi fungsi g o f dapat didefinisikan dengan (g o f)(x) = g(f(x)) = g (2x) = (2x)3 = 8x3
= Dg maka komposisi fungsi g o f dapat didefinisikan dengan (g o f)(x) = g(f(x)) = g (2x) = (2x)3 = 8x3
Kasus f o g
Karena Rg 
 = Df maka komposisi fungsi f o g dapat didefinisikan dengan (f o g)(x) = f(g(x)) = f(x3) = 2x3
= Df maka komposisi fungsi f o g dapat didefinisikan dengan (f o g)(x) = f(g(x)) = f(x3) = 2x3
Contoh 2 :
Misalkan f : 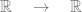 dengan f(x) = 2x, g :
dengan f(x) = 2x, g : 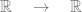 dengan g(x) = 3x dan h :
dengan g(x) = 3x dan h : 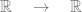 dengan h(x) = x3. Tentukan formula (f o g) o h dan f o (g o h).
dengan h(x) = x3. Tentukan formula (f o g) o h dan f o (g o h).
Penyelesaian :
(f o g)(x) = f(g(x))
= f(3x)
= 2(3x)
= 6x
((f o g) o h)(x) = (f o g)(h(x))
= (f o g)(x3)
= 6x3
(g o h)(x) = g(h(x))
= g(x3)
= 3x3
(f o (g o h))(x) = f((g o h)(x))
= f(g(h(x)))
= f(3x3)
= 2(3x3)
= 6x3
Dari Contoh 1 dan Contoh 2 diperoleh sifat-sifat Komposisi Fungsi sebagai berikut:
-
(g o f)(x) 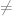 (f o g)(x) (tidak berlaku sifat komutatif)
(f o g)(x) (tidak berlaku sifat komutatif)
-
((f o g) o h)(x) = (f o (g o h))(x) (sifat asosisatif)
Untuk sifat yang kedua, perhatikan pembuktiannya.
Didefinisikan fungsi f, g dan h sebagai berikut, misalkan f : 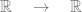 , g :
, g : 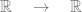 dan h :
dan h : 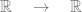 .
.
((f o g) o h)(x) = (f o g)(x) o h(x)
= f(g(x)) o h(x)
= f(g(h(x)))
= f((g o h)(x))
= f(x) o (g o h)(x)
= (f o (g o h))(x)
((f o g) o h)(x) = (f o (g o h))(x)  Sumber :
Bahri, S., 2006, Logika dan Himpunan, Universitas Mataram, Mataram.
Sumber :
Bahri, S., 2006, Logika dan Himpunan, Universitas Mataram, Mataram.
About these ads
